Hoe statistiek het schoolexamen verdacht maakte
en waarom schoolexamens dat niet verdienen
Als er geen coronacrisis was geweest zouden morgen de eerste centrale examens beginnen. Maar op 24 maart is besloten dat dit jaar alleen het resultaat van het schoolexamen telt voor het behalen van het diploma. Het onderwijsveld was blij met de duidelijkheid die het besluit gaf, maar het resulteerde ook in krantenkoppen als ‘ Is de kwaliteit van het diploma nog wel gegarandeerd’ (Trouw) en ‘wat is mijn diploma straks nog waard’? (Volkskrant).
Deze vragen komen niet uit de lucht vallen. In 2018 hebben we het incident gehad met afgekeurde schoolexamens bij een vmbo-school in Maastricht. Hierdoor heeft de Inspectie nu versterkte aandacht voor het zorgvuldige verloop van schoolexamens. Maar al sinds de invoering van de Mammoetwet in 1963 laait periodiek de discussie op over de kwaliteit van schoolexamens op (zie rapport van de commissie kwaliteit schoolexaminering voor een samenvatting). De felste discussies speelden hierbij rond de grote verschillen die er tussen scholen zijn in hoe cijfers op het schoolexamen en het centraal examen zich tot elkaar verhouden.
Wij doen sinds kort onderzoek naar de relatie tussen cijfers op het schoolexamen (SE) en het centraal examen (CE). Dit doen we aan de hand van de examengegevens van alle leerlingen zoals die geanonimiseerd zijn opgeslagen in de Nationaal Cohortonderzoek Onderwijs dataset. Uit ons onderzoek komt een veel rooskleuriger beeld van de kwaliteit van schoolexamens naar voren dan tot nu toe is gepresenteerd in andere studies. We brengen daarom vandaag graag onze bevindingen versneld naar buiten.
Het verschil tussen cijfers op schoolexamens en centrale examens
Voor we onze eigen analyses presenteren, blikken we eerst eens terug op waar de telkens terugkerende discussie over de kwaliteit van schoolexamens nu eigenlijk op gestoeld is. De meest invloedrijke criticus van schoolexamens was Prof. Jaap Dronkers, ook bekend van de scholenranglijsten die in het dagblad Trouw van 1997 tot 2012 werden gepubliceerd. Daarnaast heeft Dronkers veel onderzoek gedaan naar de relatie tussen SE- en CE-cijfers op verschillende scholen. De graadmeter die hij bij het vergelijken van scholen gebruikte was het verschil tussen het cijferlijstgemiddelde op het SE met het cijferlijstgemiddelde op het CE van alle leerlingen op een school. Dit verschil noemde hij de discrepantie tussen SE en CE cijfers, en is onder die naam een eigen leven gaan leiden in het Nederlandse voortgezet onderwijs.
Dronkers liet zien dat voor deze discrepantie een grote variatie tussen scholen bestaat, waarbij enkele scholen een discrepantie hadden van bijna een heel examenpunt. In een rapport uit 2006 (met de omineuze titel: Hoe gelijkwaardig blijft het eindexamen tussen scholen?) werden verschillen in discrepanties tussen SE en CE cijfers van scholen (met naam en toenaam genoemd) gepresenteerd en de zorgen hierover besproken. Deze bevindingen kregen veel aandacht in de media, en leidden tot alarmistische koppen als waarde middelbare schooldiploma op de tocht (Volkskrant) en diploma’s middelbare school ongelijkwaardig. (Trouw).
De zorg van Dronkers zat hem met name in dat bij scholen die een laag gemiddeld eindexamenresultaat hadden op het CE de discrepantie tussen SE- en CE-cijfers juist vaak hoger is. Hij vermoedde dat op sommige minder goede scholen leerlingen via het SE aan een diploma werden geholpen: docenten/scholen zouden SE’s expres makkelijker maken om lage CE-cijfers te compenseren.
De SE-CE discrepantie is in 2010 opgepakt door de Inspectie van het Onderwijs. De inspectie ging het als een kwantitatieve maat gebruiken voor de beoordeling van de onderwijsresultaten van een school. Voortaan gold dat het driejarig gemiddelde voor het volwaardig schoolexamen niet meer dan 0,5 punt hoger mocht zijn dan de score van de school op het centraal examen. Een groter verschil kon betekenen dat de school, na onderzoek van de inspectie, het oordeel ‘zwak’ of ‘zeer zwak’ kreeg (zie onderzoeksrapport commissie kwaliteit schoolexamens).
Sturing op het verschil tussen SE- en CE-cijfers
Het effect van dit dreigement was dat schoolleidingen bij een hoge discrepantie tussen SE en CE docenten gingen aansturen om resultaten op schoolexamens in de pas te laten lopen met die op centrale examens. Dit zou de discrepantie van de school dan verlagen. De discrepantie werd ook een zelfstandig onderzoeksonderwerp, zoals in een masteronderzoek naar welke maatregelen nu effectief zijn om het discrepantie effect te verlagen of een WODC-studie naar of leerlingen met migratie-achtergrond een extra grote discrepantie hebben.
Er kwam al snel tegengas. Met name de vaksecties moderne vreemde talen maakten zich zorgen over het effect dat sturen op de discrepantie had op de inhoud van het taalonderwijs en op de motivatie van taaldocenten. Vanuit de vaksecties en het ministerie van onderwijs is hierover een onderzoeksrapport uitgebracht, waaruit bleek dat de meerderheid van de schoolleiders docenten aanstuurt op basis van verschillen tussen cijfers voor het SE en CE. Hierbij werden vooral intensivering van de training voor het centrale examen (leesvaardigheid), maar ook gewoon de suggestie om in het vervolg minder hoge cijfers te geven op schoolexamens.
Sinds kort weegt de onderwijsinspectie de discrepantie tussen SE- en CE-cijfers niet standaard meer mee bij het oordeel over de onderwijsresultaten (zie examenbesluit). De SE-CE verschillen worden wel nog steeds voor ieder vak gepubliceerd, en de inspectie kan het nog mee nemen in haar onderzoeken. Op scholen wordt het hierdoor nog steeds vaak besproken bij de evaluatie van de kwaliteit van schoolexamens.
De relatie tussen CE- en SE-cijfer in het VO.
Maar zijn de zorgen terecht? Bij het nadenken over manieren om de relatie tussen CE-SE cijfers te onderzoeken kwamen wij tot onze schrik tot de conclusie dat het gehele onderzoek naar SE-CE discrepantie een pijnlijke dwaling is geweest, met grote invloed op de beeldvorming over schoolexamens. Onze analyses van examendata geven aan dat de discrepanties tussen SE- en CE-cijfers op leerling- en op schoolniveau wel enorm verschillen, maar dat deze verschillen hun bron niet hebben in de kwaliteit van de examens maar eerder voortspruiten uit de statistische verdeling van SE en CE-cijfers. Om dit uit te leggen nemen we je graag even mee in de statistiek van SE- en CE-cijfers en de relaties die hiertussen bestaan.
Als je de cijfers van leerlingen op het CE en het SE wilt vergelijken dan is het meest simpele om de twee gemiddelden tegen elkaar af te zetten, zoals Dronkers deed. Maar achter een gemiddelde schuilt een hele verdeling van cijfers die door leerlingen zijn gehaald. Als de examencijfers van iedere leerling door een groot aantal factoren wordt beïnvloed zoals ijver, kwaliteit van de school, intelligentie, virusinfecties, ambities in de omgeving, etc., dan zal deze verdeling van de cijfers een normaalverdeling De normaalverdeling geeft aan welke fractie van de leerlingen een bepaald cijfer heeft gehaald. Een normaalverdeling wordt gekarakteriseerd door zijn gemiddelde (en dat is ook de meest voorkomende waarde) en door de standaarddeviatie of standaardafwijking - dat is een maat voor de breedte van de cijferdistributie (binnen het interval gemiddelde +/- 1 standaarddeviatie vallen 68% van de waarnemingen). volgen.
In figuur 1 hebben we de normaalverdeling getekend voor een typisch CE en SE. De examengemiddelden wijken wat af van elkaar (6,3 vs 6,5) maar opvallender is dat de spreiding van de cijfers, oftewel de standaarddeviatie verschilt tussen de soorten examens: de verdeling van CE-cijfers is breder dan die op het SE.
Dit is te verklaren uit het feit dat het SE niet echt een examen is: het SE is voor bijna alle scholen en alle vakken een gemiddelde van een aantal beoordelingen. Deze beoordelingen toetsen allemaal verschillende onderdelen van een vak, en elke leerling heeft wel een onderdeel waar hij of zij hoger of lager op scoort dan op het andere. Het gevolg daarvan is dat extreme SE-cijfers worden weggemiddeld. Een SE-toets die op een goede dag tot een hoog cijfer leidt, wordt meestal gecompenseerd door een andere SE-toets of een slechtere dag, of beoordeling over een onderdeel van het vak waar je minder in uitblinkt.
Bij het centrale examen gaat die vlieger niet op. Voor elk vak is er maar één dag waarop de leerling zich kan bewijzen. Op die dag van het CE kan een leerling iets onder of boven zijn niveau presteren, uitglijden, of juist ineens gigantisch boven zijn eerdere niveau uitstijgen – extreme cijfers zijn dus mogelijk. Dit vertaalt zich in het voorbeeld van Figuur 1 boven in een standaarddeviatie van 0,5 punt voor de SE-cijfers en 0,7 voor CE-cijfers.
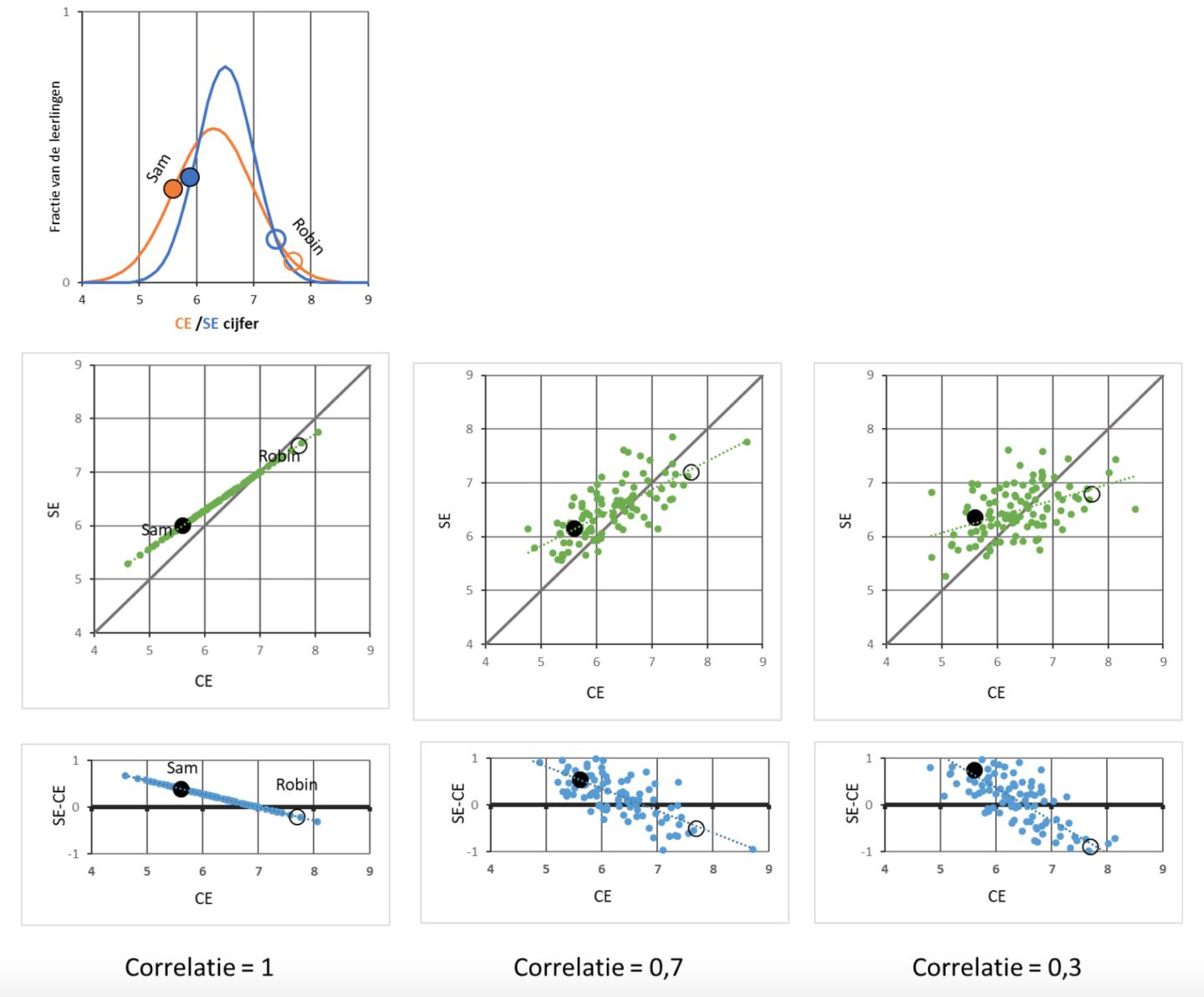
De spreiding van de cijfers voor het schoolexamen is dus kleiner dan die van het centraal eindexamen, wat zou dat? Laten we nu eens twee hypothetische leerlingen volgen die het schoolexamen en centraal examen gemaakt hebben. Als eerste nemen we Robin. Robin was een bijzonder goede leerling, en had een schoolexamengemiddelde dat wel twee standaardafwijkingen hoger was dan het gemiddelde, dus een 6,5 + 2 x 0,5 = 7,5. Sam was juist vaak net wat minder goed dan het gemiddelde en had een SE-cijfer dat 1 standaardafwijking lager was dan het gemiddelde, d.w.z. 6,5 – 0,5 = 6,0. Vervolgens gaan Sam en Robin het centraal examen in.
Stel nu dat het centraal examen en schoolexamen een perfecte samenhang hebben. Hiermee bedoelen we dat de beste leerlingen op het schoolexamen ook altijd weer de beste leerlingen op het centraal examen zijn en dat de volgorde daarachter ook constant blijft. Robin heeft dan op het CE ook weer een cijfer dat 2 standaarddeviaties hoger is dan het gemiddelde, voor het CE is dat dan 6,3 + 2 x 0,7 = 7,7. Het CE-cijfer van Robin is dus 0,2 punt hoger dan het SE-cijfer (7,7 – 7,5 = 0,2). Voor Sam geldt dat het cijfer nog steeds 1 standaarddeviatie lager uitkomt dan het gemiddelde en voor het CE-examen is dat dan 6,3 – 1 x 0,7 = 5,6. Het CE cijfer van Sam is dus juist 0,4 punt lager dan het SE-cijfer (5,6 – 6,0 = -0,4). Dit voorbeeld is geïllustreerd in figuur 1.
Natuurlijk zijn leerlingen nooit precies even veel standaarddeviaties weg van het gemiddelde voor zowel CE als SE. Als dit zo was, dan zou het centraal examen voor niemand echt spannend meer zijn. In de praktijk hebben leerlingen met een hoog SE-cijfer ook wel eens een tegenvallend resultaat en leerlingen met een laag SE halen soms een veel hoger cijfer op het CE: SE en CE hangen niet helemaal perfect samen.
Hoe sterk twee variabelen (lineair) met elkaar samenhangen kan worden weergegeven met de zgn. correlatie-coëfficient Een correlatie kan in waarde variëren tussen –1 en +1. Daarbij betekent 0: geen lineaire samenhang, +1: een perfecte positieve lineaire samenhang en –1: een perfecte negatieve lineaire samenhang. Een correlatie van 1 geeft dus aan dat de waarde voor het andere cijfer volledig bepaald wordt door het eerste. . In Figuur 1, tweede rij, laten we het verband tussen CE- en SE-cijfers zien voor 100 gesimuleerde Cijfers van reëel bestaande leerlingen mogen we hier niet laten zien uit privacy-overwegingen. leerlingen als de samenhang perfect is (correlatie 1), sterk (correlatie 0,7) en zwak (0,3) is. Perfecte samenhang komt niet voor bij examens, maar er zijn wel vakken waar de correlatie tussen CE en SE sterk is of net zwak (later in dit artikel komen we daarop terug). Hoe lager de correlatie, hoe meer de punten van de lijn kunnen afwijken, en hoe meer de rechte trendlijn Van de vorm, SEi= a x CEi + b. afvlakt. Deze afvlakking zorgt ervoor dat de afwijking van de gemiddelde lijn door de punten aan de randen telkens meer gaat afwijken van de grijze lijn die de situatie weergeeft waarin CE- en SE-cijfers aan elkaar gelijk zijn.
Op de onderste rij wordt het verschil tussen CE en SE weergegeven, feitelijk de afstand tussen elk punt in de middelste rij en de grijze lijn (CE=SE). Dit is de discrepantie tussen SE en CE van individuele leerlingen (op de x-as CE, op de y-as SE min CE). Te zien is dat de discrepantie gemiddeld positief is (hoger SE dan CE) voor leerlingen met een laag CE, en negatief (lager SE dan CE) voor leerlingen met een hoog CE. Dat zagen we boven al voor Robin en Sam: Robin heeft een grotere kans op een hoger CE dan SE en Sam heeft meer kans op een lager CE dan SE. In de onderste rij is te zien dat de discrepanties tussen SE en CE cijfers bij zowel lage als hoge CE-cijfers sterker worden voor lagere correlaties dan 1. In de middelste rij is dat te zien als een groter gat tussen de puntenwolk en de grijze lijn bij lagere correlaties
De formule voor verwachtingswaarde voor een schoolexamencijfer SE_i op basis van een cijfer op het centraal examen CE_i staat in het figuur. Hierbij staat μ voor gemiddelde en σ voor de standaarddeviatie. Dit is ook de formule waarmee we de cijfers van Sam en Robin hebben berekend hebben. Bij een correlatie van 0,7 en 0,3 komen de punten zo op de trendlijn door de puntenwolk terecht. De puntenwolk in Figuur 1 is gegenereerd met de verdelingen die aan de top van de figuur werden getoond, en onder aanname van een lineair verband met de aangegeven correlatie.
.
De crux, nu, is dat het voor scholen precies zo werkt: als een school gemiddeld veel leerlingen heeft met een laag CE, zal die school vanzelf een positieve discrepantie hebben, net als Sam een hoger gemiddeld SE dan CE Dit volgt uit het feit dat de verwachting van een (school)gemiddelde gelijk is aan het gemiddelde van de verwachtingen. Met andere woorden, als bij de meeste leerlingen, zoals bij Sam, er een discrepantie verwacht kan worden tussen SE- en CE-cijfer, dan is dat op schoolniveau ook zo. . De discrepanties waar Dronkers (en de Inspectie) kwade wil achter vermoedde(n), zijn dus een statistisch artefact. Kort samengevat: een kleinere standaarddeviatie van het SE, en een niet-perfecte correlatie tussen SE en CE, zorgen er samen voor dat er vanzelf een discrepantie ontstaat tussen CE- en SE-gemiddelden op schoolniveau. En wel precies de discrepantie die Dronkers zo verdacht vond.
SE-CE discrepanties in de praktijk
In figuur 2 hebben we de discrepantie uitgezet tussen het CE- en SE- gemiddelde voor vwo- en havo -afdelingen van alle VO-scholen van Nederland in 2014 en 2015. Naast de verdeling staat de voorspelling aangegeven van de discrepantie zoals we die we hebben afgeleid uit het CE-gemiddelde van de school, de correlatie tussen CE en SE, en de standaarddeviaties van CE en SE (op schoolniveau).
In Figuur 2 is te zien dat het verschil tussen SE- en CE-cijfers groter is voor scholen met een laag CE-gemiddelde, precies zoals Dronkers ook vond. Maar als je die discrepantie vergelijkt met de verwachting die we kunnen berekenen met onze formule, blijkt de overeenkomst juist heel goed. Het CE-gemiddelde van de school, de correlaties en standaarddeviaties verklaren samen de discrepantie tussen SE en CE cijfers. Natuurlijk is er binnen iedere groep met een bepaald CE-gemiddelde nog wel een spreiding over, maar die is laag (ongeveer ± 0,2 pt rond de voorspelde waarde). Hoewel we het hier niet tonen blijkt dit precies zo uit te pakken voor de examens van de verschillende vakken .
Of er nu niet toch ook een systematisch verschil is in het verband tussen CE- en SE-cijfers voor leerlingen op een school met een hoog CE-gemiddelde of een laag CE-gemiddelde – in andere woorden: de suggestie dat docenten op scholen met een laag CE-gemiddelde hun leerlingen ‘ een handje zouden helpen’ bij het halen van het examen door ze hogere SE cijfers te geven – hebben we ook bekeken. In figuur 3 tonen we het verband tussen CE-cijfers en SE-cijfers van individuele leerlingen, uitgesplitst voor de 10% leerlingen op scholen met de hoogste CE-gemiddelden in 2014 en 2015, voor de 10% leerlingen op scholen met de laagste CE-gemiddelden, en de 10% middelste scholen (leerlingen tussen 45% en 55% van de rangordening op CE- schoolgemiddelden).
In figuur 3 (rechts) is de cijferverdeling te zien van leerlingen op deze drie groepen scholen. Hier blijkt dat op alle scholen leerlingen voorkomen die hogere of lagere CE-cijfers halen. Natuurlijk verschuift de curve wel naar hoge cijfers voor leerlingen op scholen met een hoog CE-gemiddelde, maar er is ook flinke overlap in het midden van de verdelingen. In figuur 3 (links) laten we zien wat het gemiddelde SE-cijfer is voor leerlingen die een bepaald CE-cijfer hebben behaald. De punten blijken verbluffend dicht bij elkaar te liggen voor de drie groepen scholen: voor leerlingen met een CE-gemiddelde van 6,1, varieert het SE-gemiddelde rond de 6,3, of je nu naar leerlingen op een school met een hoog of met een laag CE-gemiddelde kijkt.
Het is de moeite waard even te bedenken hoe figuur 3B eruit had gezien als Dronkers gelijk had gehad. Als ‘zwakke’ scholen hun SE makkelijker hadden gemaakt om leerlingen te helpen, zouden alle leerlingen op die scholen een hoger SE-gemiddelde hebben – leerlingen zouden daar immers allemaal te makkelijke toetsen maken. Met andere woorden, de blauwe punten zouden ver boven de gele en oranje punten moeten liggen, en wel precies even veel als de discrepantie die Dronkers vond tussen CE- en SE-cijfers (oplopend tot een heel punt!). Daar is geen sprake van: er is een afwijking van ongeveer +/- 0,1 pt van de blauwe met de oranje en gele punten. De zwarte lijn die onze voorspelling op basis van de verdelingen van SE en CE-cijfers weergeeft, gaat dwars door het midden van de puntenwolk, weer illustrerend hoe goed de voorspelling bij de data past.
Rechtsboven in de figuur zie je dat leerlingen met een hoog CE-cijfer vaak een hoger SE-cijfer hadden dan de lijn van het model. We hebben uitgezocht dat dat dan waarschijnlijk verklaard kan worden met een iets hogere correlatie tussen SE- en CE-cijfers voor deze groep leerlingen, waardoor de SE-CE lijn iets minder “afvlakt” dan voor de rest van de leerlingen (zie Figuur 1).
De relatie tussen CE- en SE cijfer bij verschillende schoolvakken
Tot slot hebben we de samenhang tussen CE- en SE-cijfers bij verschillende vakken bekeken. In Figuur 4 zie je voor ieder vak wat de correlatie is tussen het SE en CE van dat vak op het havo en het vwo is. We hebben dit uitgerekend over de periode 2012-2016 en het blijkt dat deze correlatie ieder jaar min of meer gelijk is. Aan deze correlatie moet niet direct een waardeoordeel van kwaliteit worden gehangen. Het geeft alleen aan in hoeverre het resultaat van leerlingen op het SE lijkt op die op het CE van hetzelfde vak. Dit verband blijkt op het vwo over het algemeen wat sterker te zijn dan op de havo. Nederlands heeft een opvallend lage correlatie op zowel het havo als het vwo.
In Figuur 5 geven we de correlatie van alle examenonderdelen met het eindcijferlijstgemiddelde (gemiddelde CE-SE cijfer over alle vakken) van de leerlingen op het havo en het vwo.
Vanzelfsprekend is in Figuur 5 de correlatie hoog tussen de SE- en CE-gemiddelden van de leerlingen en hun eindcijfer (ongeveer 0,9). Het SE en CE bepalen namelijk ieder voor 50% het gemiddelde van de eindcijferlijst en zijn dus beiden goede voorspellers van het eindcijfer op het diploma. Voor alle andere vakken (behalve Duits en Frans) blijkt op zowel het havo als het vwo dat het SE telkens wat sterker correleert met het cijferlijstgemiddelde dan het CE-cijfer. Als je samenhang met andere cijfers ziet als een kwaliteitskenmerk (en daar valt veel voor te zeggen), zijn dus niet de CE’s de betere metingen van het kunnen van leerlingen, maar SE’s!
Niet dat hiermee alles gezegd is Voor vakken als bijvoorbeeld Duits en Frans is de correlatie met het cijferlijstgemiddelde relatief laag (Figuur 5), maar de onderlinge correlatie is juist hoog (Figuur 4, vwo-niveau). Dit betekent dat je gewoon goed in Duits of Frans kunt zijn, en dat dat niet meteen impliceert dat je goed in andere vakken bent. Maar met een slecht cijfer op het SE Duits haal je over het algemeen niet een hoog cijfer op het CE Duits.
Conclusies
Recent heeft de commissie kwaliteit schoolexaminering geschreven dat sturing op de discrepantie van Dronkers negatief heeft uitgepakt voor hoe scholen omgaan met schoolexamens. Gelukkig gebruikt de Inspectie dat inmiddels ook niet direct meer als beoordelingsinstrument voor scholen. Wat wij hopen te hebben laten zien is dat die discrepantie een statistisch artefact was, een onvermijdelijk bijproduct van een niet-perfecte correlatie tussen SE en CE en een ongelijke standaarddeviatie. Het verschil tussen SE- en CE-cijfers kan daarom nooit een goede kwaliteitsmarker zijn voor het niveau van de examinering. Onze analyses laten zien dat we de verschillen tussen SE- en CE-cijfers bijna volledig kunnen verklaren uit statistische eigenschappen van het SE en CE. Er blijft maar een uiterst klein verschil over waar het gaat om SE-cijfers die leerlingen krijgen op scholen waar de resultaten juist het hoogst, of juist het laagst zijn (zie figuur 3).
De focus op de discrepantie tussen SE en CE cijfers heeft als uitwerking gehad dat de examinering van scholen met een minder hoog CE-gemiddelde verdacht werden, omdat het SE hoger was dan het CE. Dit terwijl scholen metde meest kansrijke leerlingen heel makkelijk als winnaar uit de bus kwamen, omdat het CE gemiddelde juist hoger was dan het SE.
Dit was allemaal niet terecht en kan toch nooit de bedoeling zijn geweest? Wat betekent dit nu voor examinering in het Nederlandse voortgezet onderwijs? Om te beginnen mogen we weer meer vertrouwen hebben in hoe op verschillende scholen schoolexamens worden georganiseerd en becijferd. Onze analyses geven hier alle aanleiding toe. Scholen en docenten kunnen uitgaan van hun eigen kracht. Ze zouden zich vrij moeten voelen om de ruimte (die er zeker is!) te gebruiken voor een schoolexamen dat past bij hun onderwijsvisie.
Tegenwoordig moeten leerlingen ook op het CE een 5,5 gemiddeld halen om te slagen. Dit geeft ook verantwoordelijkheid voor een deugdelijk centraal examen dat goed in elkaar zit en uitpakt zoals we wenselijk vinden. Een wel hele lage correlatie tussen CE en SE van het kernvak Nederlands op de havo en het vwo geeft te denken. Andere relaties tussen SE- en CE-onderdelen lijken robuust en hebben waarden die waarschijnlijk binnen het systeem van een gedeeld school- en centraal examen wenselijk zijn.
De nationale standaard van het centrale examen is voor iedereen hetzelfde, ongeacht je leraar of school. Het schoolexamen geeft scholen de verplichting en de vrijheid om allerlei andere dingen aan de orde te laten komen. Wat we hier precies over afspreken kunnen we zo nu en dan afstemmen op voortschrijdend inzicht en veranderende wensen. Voor dit bijzondere jaar kunnen we concluderen dat schoolexamens in Nederland deugdelijk zijn, en het prima een jaartje kunnen rooien zonder centrale examens.
